Launching something new looks exciting from the outside, but...
The digital landscape is evolving faster than ever, and...
New Zealand has emerged as one of the most...
Living in a studio apartment often means dealing with...
Shearling jackets have made it to their places as...
New Launch Flats & Apartments in Ahmedabad Ahmedabad has...
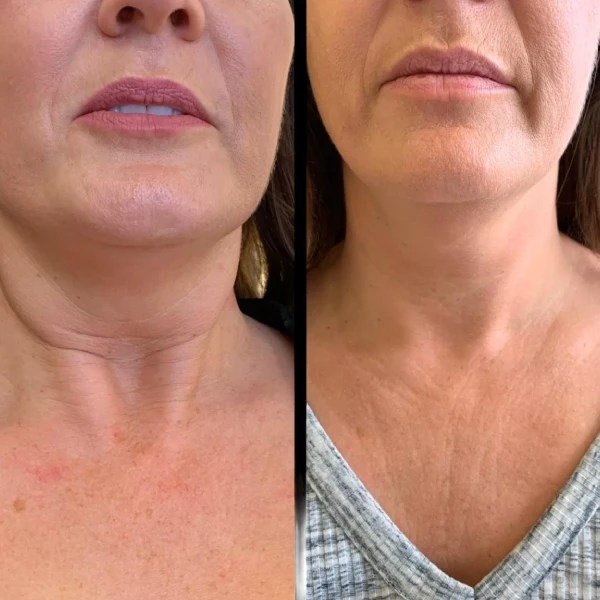
Juvederm treatments have become one of the most popular...
The death of a human being was and continues...
Best Doctors in Dubai and the Philosophy of Natural...
Understanding Breast Lift in Dubai: A Comprehensive Overview A...